2けたの掛け算ー暗算のコツ
2桁の掛け算の暗算のコツをまとめました。
①20未満の2桁同士の場合。(45通り)
例えば12×13の場合、下の左側の図を思い浮かべる。
10×2の青い部分を、下の右側の図のように移動して10×(10+3+2)を計算する。
余っている緑の部分3×2を足す。そうすると150+6=156と計算できる。
②10の位が同じで1の位の和が10の場合。(45通り)
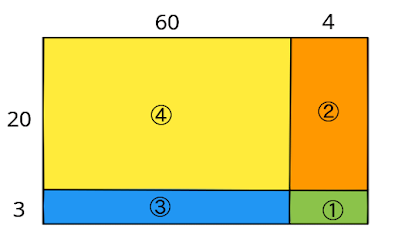
例えば64 × 66の場合、下の左の図を思い浮かべる。
60 × 4の青い部分を、下の右の図のように移動して60×70で計算する。
余っている緑の部分、6×4を足す。そうすると4200+24=4224と計算できる。
③10の位の和が10で1の位が同じ場合。(45通り)
例えば22 × 82の場合、10の位同士をかけて1の位を足す。2 × 8 + 2 = 18
その数に100をかけたものに、1の位同士をかけた数を足す。18 × 100 + 2 × 2 =1804
④91以上の2桁同士の場合。(45通り)
⑤1の位の和が10で10の位が1つ違いの場合。(71通り)
(a + b)(a – b) = a²- b²の公式を利用する。
例: 57×43 =
(50+7)(50-7) = 2500 – 49 = 2451
⑥片方が11の場合。
11ではない方の数字に着目し、1の位はそのまま1の位、10の位を100の位に持っていき、10の位と1の位を足した数字を10の位に持っていく。(81通り)
⑦99を含む場合。(81通り)
a×99=a(100-1)=100a-aに変形する。
例:24×99 = 24 ×100 – 24 = 2376
※千の位・百の位は(a-1)、10の位・1の位は(100-a)となると考えることもできる
例:45 × 99 45-1=44 ,100-45=55 なので
4455
⑧1の位が9を含む場合(693通り)
a×b=a(b+1)-aの形にする。
例:23×39=23×(40-1)=23×40-23=920-23=897
⑨同数同士のかけ算の場合。
⑩上記以外
少し難しいが下記の方法で暗算できる。
例:23 × 64
①1の位同士を掛ける:3 x 4 = 12
②1の位を0にし2番目の数の1の位と掛け、①と足す:20 x 4 = 80 80+12=92
③1の位と2番目の数の1の位を0にしたものを掛け、②と足す:3 x 60 = 180 180+92=272
④両方の数の1の位を0にしたものを掛け、③と足す:20 x 60 = 1200 1200+272=1472





コメント
1 件のコメント :
う〜ん暗算の方式⁉️理解し覚える方が難解😱これを考える人の脳は一体どういう感じ〜🧠は使わなければ失われると言われるけど、、会得し瞬時に計算できるって凄いね❣️🧠小宇宙なんて表現される様にのびしろは無限なんかね⁇👵高度な情報感謝🙇♀️
コメントを投稿